1. Überprüfung des physikalischen Prinzips der Kernformel
Gesetz der Massenerhaltung
Alle Formeln basieren auf der physikalischen Natur von m=ρ×V (Masse = Dichte × Volumen)
Dichtewert
Theoretische Dichte von reinem Aluminium: 2,698 kg/m³ (20℃)
Der Richtwert von 2.700 kg/m³ ist für industrielle Berechnungen sinnvoll (Fehler < 0,1%)
2. Überprüfung der Strenge geometrischer Formeln
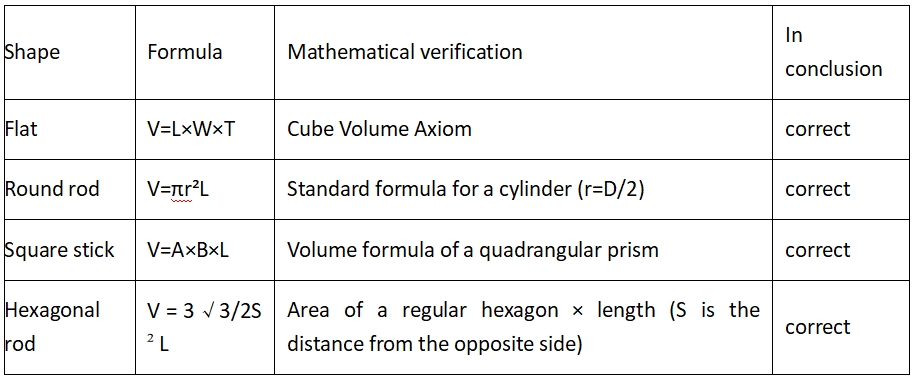
2.1. Standardformel für das geometrische Volumen
Einschränkungen der Vierkantrohrformel:
Dies gilt, wenn die Rohrwandstärke gleichmäßig ist und der Innenwinkel ein rechter Winkel ist (das tatsächliche Vierkantrohr hat einen abgerundeten Übergang und der theoretische Fehler beträgt etwa 1–3 %)
3. Überprüfung der Einheitssystemkonsistenz
Einheitenübergreifende Berechnung Risikopunktuntersuchung
4. Änderung der technischen Eignung
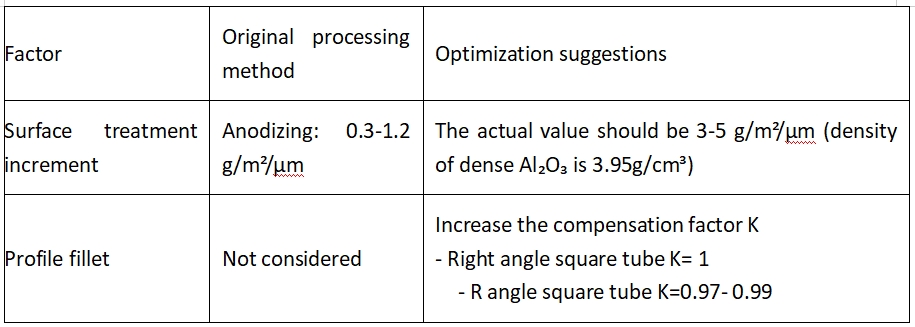
4.1. Kompensation nicht idealer Faktoren
4.2. Quantifizierung der Toleranzauswirkungen
Dickentoleranz ±10 % → Gewichtsabweichung ±(8 % ~ 12 %) (dünnwandige Teile sind empfindlicher)
Lösung: W tatsächlich = W theoretisch × (1 + Δt / t) ( Δt : Dickenabweichung)
5. Randbedingungstest
Überprüfung im Extremfall:
Dichteanomalieszenario
7xxx-Legierung (7075): Gemessene Dichte 2,810 g/cm³ → Wenn irrtümlich 2,7 g/cm³ verwendet wird, beträgt der Fehler +4,1 %.
Formeltabelle
4t(A + B)- 4t² ist eine standardmäßige technische Berechnung, die durch Multiplikation des Umfangs des Abschnitts mit der Wandstärke und anschließendem Abzug der vier Ecken berechnet wird.
Berechnungsbeispiel:
1.6061 Aluminiumplatte(1000 × 500 × 10 mm, Länge 2 m): W = 1000 × 500 × 2 × 0,0027 = 27 kg
2.7075 Rundrohr(Außendurchmesser 50 mm, Wandstärke 3 mm, Länge 1,5 m): W = [(50-3)×3×3,1416×1,5]×0,00283 ≈ 5,65 kg
3. Vierkantrohr(40×40×2mm, Länge 3m): W = [2×2×(40+40-4)×3]×0,0027×0,98 ≈ 2,42 kg
Empfohlener Arbeitsablauf
1. Dichte auswählen → 2. Tatsächliche Größe messen → 3. Kompensationsfaktor auswählen → 4. Nach Formel berechnen
Veröffentlichungszeit: 17. Juni 2025